上篇 blog 中过了一下 VAE 的 intuition,还是很直白的,不过看介绍 VAE 背后的数学的文章总是觉得有点缺少连接感,于是除了吃饭睡觉都看数学(误)推了两个星期算是把公式推通了。感觉整个流程对我这种数学基础不好的来讲还挺吃力,在这里记录一下。
前置准备
在推公式之前,先把用到的数学公式复习/预习一下,后面就直接套进去就好。
概率的期望
可以用抽奖的例子来快速回忆起来概率的“期望”的概念:假如参加抽奖活动有一等奖和二等奖两种奖项,一等奖的概率是 1%,奖金 10000,二等奖的概率是 10%,奖金 100,问我参加这个抽奖活动可以赢得的奖金的期望是多少?
$$ \mathbb{E}[x] = \sum_{i=1}^{n} x_i p_i(x_i) $$其中 $x$ 是随机变量,$x_i$ 对应不同奖项的奖金,$p_i(x_i)$ 是对应不同奖项的概率。在这个例子中,我们抽奖得到奖金的期望是 $10000 \times 0.01 + 100 \times 0.1 = 110$。
对于连续的随机变量,期望的计算就是:
$$ \mathbb{E}[x] = \int x p(x) dx $$期望也可以通过采样的方法来估计,比如我们有一个样本集合 $X = \{x_1, x_2, \ldots, x_n\}$,那么期望可以这样估算:
$$ \mathbb{E}[x] \approx \frac{1}{n} \sum_{i=1}^{n} x_i, \,\,\,\, x_i \sim p(x) $$在推导中,我们可以借助这个换算,把连续的期望转换为采样的离散计算:
$$ \begin{align*} \mathbb{E}[x] &= \int x p(x) dx \\ &\approx \frac{1}{n} \sum_{i=1}^{n} x_i, \,\,\,\, x_i \sim p(x) \end{align*} $$比较典型的采样计算就是,在机器学习的一轮训练中,我们手里有一批训练数据集,就可以通过这组数据集作为样本集合来估算出期望的值。
期望的计算也可以代入到函数中:
$$ \begin{align*} \mathbb{E}[f(x)] &= \int f(x) p(x) dx \\ &\approx \frac{1}{n} \sum_{i=1}^{n} f(x_i), \,\,\,\, x_i \sim p(x) \end{align*} $$这里代入的函数一般就是 $\ln$,在概率分布是正态分布时,代入正态分布的公式可以最后推导为最小二乘法,这就和我们常见的损失函数联系起来了,在后面的推导中我们会具体地看到这个过程。
正态分布
正态分布也称作高斯分布,也就是我们常说的钟形曲线:
$$ \mathcal{N}(\mu, \sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(x - \mu)^2}{2\sigma^2}\right) $$假如人的身高符合高斯分布,那么我们可以用高斯分布的公式来计算一个人一米八的概率是多少。
在 VAE 中,隐变量、编码器与生成器的输出均设定为满足正态分布,在它们的推导也都会用到正态分布的公式。
KL 散度
KL 散度能够用来衡量两个概率分布之间的差异,定义如下:
$$ \text{KL}(p||q) = \int p(x) \log \frac{p(x)}{q(x)} dx $$KL 散度有一个性质就是总是大于零,在计算 $\text{ELBO}$ 作为下界时有用到这个性质。
根据苏神的博客里的说法,KL 散度也并非衡量两个概率分布的唯一办法,但是 KL 散度可以写成期望的形式,这在 VAE 的推导里面会比较方便。
当比较两个正态分布的 KL 散度时,可以直接带入如下公式:
$$ \begin{align*} \text{KL}(P || Q) &= \text{KL}(\mathcal{N}(\mu_P, \sigma_P^2) || \mathcal{N}(\mu_Q, \sigma_Q^2)) \\ &= \frac{1}{2} \left( \log \frac{\sigma_Q}{\sigma_P} + \frac{\sigma_P^2 + (\mu_P - \mu_Q)^2}{\sigma_Q^2} - 1 \right) \end{align*} $$和标准正态分布 $\mathcal{N}(0,1)$ 做比较的话,$\mu_Q = 0$,$\sigma_Q = 1$,可以进一步简化为:
$$ \text{KL}(\mathcal{N}(\mu_P, \sigma_P^2) || \mathcal{N}(0, 1)) = - \log \sigma_P + \frac{\sigma_P^2 + \mu_P^2 - 1}{2} $$贝叶斯公式
贝叶斯公式能够告诉我们如何根据新的证据(比如训练数据中的猫狗图)来调整我们对事件(某图像是合法的猫狗图片)的信念:
$$ p(z|x) = \frac{p(x|z)p(z)}{p(x)} $$在 VAE 的推导中,我们会代入贝叶斯公式来计算隐变量与正常图片之间条件概率。
图片生成模型
按概率的视角来看图片生成模型的话,我们假设 $p(x)$ 的概率分布是我们希望生成的图片的分布。
怎样理解这个概率分布?我们可以把 $x$ 对应一组 $128 \times 128$ 个像素组成的向量,对于一张有效的图片(比如猫狗照片),$p(x)$ 会接近 1,对于一张无效的乱码图片,$p(x)$ 会接近于 0。
生成图片的过程,就等于在 $p(x)$ 分布中采样。
但是 $x$ 作为一个高维度的随机变量,大部分可能的值按说都是无效的。我们不知道 $p(x)$ 的具体分布形式,我们并不知道怎样从 $p(x)$ 中采样。
针对不知道怎么采样的问题,VAE 在设定中会多安排一个隐变量 $z$,在生成图片时,我们先对正态分布的 $p(z)$ 进行随机采样,然后再通过 $p(x|z)$ 采样生成图片 $x$,使得 $p(x)$ 尽可能的接近 1。
这一来每次采样,总是能生成出有效的图片。$p(x|z)$ 也被称作解码器(Decoder)。
至于 $z$ 可以看做是对原始图片的编码,编码器(Encoder) 会对图片 $x$ 按正态分布的 $p(z|x)$ 来采样,得到一个具体的 $z$。
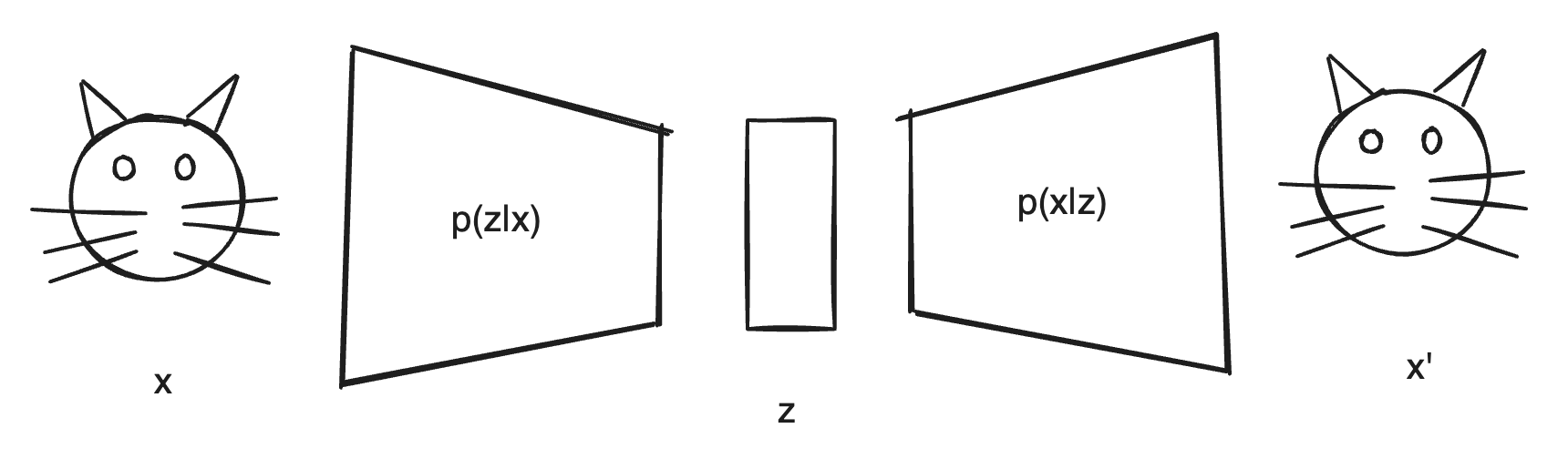
在训练的过程中,我们希望通过训练数据集 $x$ 来使 $p(x)$ 的概率最大化,从而同时学习得到一个好的编码器和解码器。在做图片生成时,就只拿解码器来用。
从最大化 $p(x)$ 到 ELBO
由于直接计算 $p(x)$ 会非常困难,VAE 在这里引入了变分推断的思想:引入一个近似的后验分布 $q(z|x)$ 使它来近似 $p(z|x)$ 的分布。我们可以把这个近似的后验分布 $q(z|x)$ 理解为神经网络拟合出来的一个概率分布。虽然我们事前并不知道 $p(z|x)$ 的具体分布,但是我们可以通过最大化 $p(x)$ 来优化 $q(z|x)$,使之接近真正的 $p(z|x)$。
推导最大化 $p(x)$ 的过程如下:
$$ \begin{align} \max p(x) &= \max \ln p(x) \\ &= \max \ln p(x) \textcolor{blue}{\underset{=1}{\int q(z|x) \, dz}} \\ &= \max \int q(z|x) \ln p(x) \, dz \\ &= \max \int q(z|x) \ln \textcolor{blue}{\frac{ p(x|z) p(z) }{ p(z|x)}} \, dz \\ &= \max \int q(z|x) \ln \frac{p(x|z) p(z) \, \textcolor{blue}{q(z|x)}}{p(z|x) \textcolor{blue}{q(z|x)}} \, dz \\ &= \max \underbrace{\int q(z|x) \ln \frac{q(z|x)}{p(z|x)} \, dz}_{KL \, Divergence} + \int q(z|x) \ln \frac{p(x|z)p(z)}{q(z|x)} dz \\ &= \max \underbrace{D_{KL} ( q((z|x) || p(z|x))}_{always\, \ge 0} + \int q(z|x) \ln \frac{p(x|z)p(z)}{q(z|x)} dz \\ &\ge \max \underbrace{\int q(z|x) \ln \frac{p(x|z)p(z)}{q(z|x)} dz}_{ELBO} \end{align} $$在 $(2)$ 和 $(3)$ 中,代入已知等于 1 的 $\int q(z|x) dz$。
在 $(4)$ 中,代入贝叶斯公式,将 $p(x)$ 变换为 $\frac{p(x|z) p(z)}{p(z|x)}$。
在 $(5)$ 中,乘入等于 1 的 $\frac{q(z|x)}{q(z|x)}$,到 $(5)$ 中可以凑出来 $q(z|x)$ 和 $p(z|x)$ 的 KL 散度。
利用 KL 散度总是大于零的性质,我们可以得到 $\ln p(x)$ 的下界,也就是 ELBO:
$$ ELBO = \int q(z|x) \ln \frac{p(x|z)p(z)}{q(z|x)} dz $$$p(x)$ 总是大于 ELBO,所以我们可以通过最大化 ELBO 来尽可能地最大化 $p(x)$。
从 ELBO 到 Training Objectives
ELBO 的式子到这里还不能直接用来训练模型,要继续推导一下:
$$ \begin{align} ELBO &= \int q(z|x) \ln \frac{p(x|z)p(z)}{q(z|x)} dz \\ &= \int q(z|x) \ln \frac{p(z)}{q(z|x)} dz + \int q(z|x) \ln p(x|z) dz \\ &= - \int q(z|x) \ln \frac{q(z|x)}{p(z)} dz + \int q(z|x) \ln p(x|z) dz \\ &= - D_{KL}(q(z|x) || p(z)) + \mathbb{E}_{z \sim q(z|x)}[\ln p(x|z)] \end{align} $$作为损失函数时,通常更喜欢朝最小化的方向去,所以我们可以把 ELBO 取负数,得到 Loss 函数:
$$ \mathcal{L} = - ELBO = D_{KL}(q(z|x) || p(z)) - \mathbb{E}_{z \sim q(z|x)}[\ln p(x|z)] $$推导的中心似乎是凑出来 $q(z|x)$ 和 $p(z)$ 的 KL 散度的式子,对应 “Divergence Loss”;其余部分正好是 $z$ 在 $q(z|x)$ 下的对 $\ln p(x|z)$ 期望,对应 “Reconstruct Loss”,到这里就和前一篇文章写的损失函数的两部分对上了。
代入正态分布
前面提到 $p(z)$、$q(z|x)$ 和 $p(x|z)$ 都是正态分布,已知 $p(z)$ 是满足 $\mathcal{N}(0, 1)$ 的标准正态分布,而 $q(z|x)$ 和 $p(x|z)$ 均来自于神经网络的拟合。
设 $q(z|x)$ 和 $p(x|z)$ 的参数分别为 $\theta$ 和 $\phi$:
$$ \begin{align*} q_\theta(z|x) &= \mathcal{N}(\mu_\theta(x), \sigma_\theta(x)^2) \\ p_\phi(x|z) &= \mathcal{N}(\mu_\phi(z), \sigma_\phi(z)^2) \end{align*} $$先看 Divergence Loss 部分,可以代入与标准正态分布 $\mathcal(0,1)$ 计算 KL 散度的公式:
$$ \begin{align*} \min_\theta \text{Divergence Loss} &= \min_\theta D_{KL}(q_\theta(z|x) || p(z)) \\ &= \min_\theta D_{KL}(\mathcal{N}(\mu_\theta(x), \sigma_\theta(x)^2) || \mathcal{N}(0, 1)) \\ &= \min_\theta - \ln \sigma_\theta(x) + \frac{\sigma_\theta(x)^2 + \mu_\theta(x)^2 - 1}{2} \end{align*} $$其中 $\sigma_\theta{(x)}$ 和 $\mu_\theta(x)$ 均来自编码器的输出。
再看 Reconstruct Loss 部分,可以代入与正态分布 $\mathcal{N}(\mu_\phi(z), \sigma_\phi(z))$ 计算期望的公式,在解码器部分,我们可以使 $\sigma_\phi(z)$ 总是一个固定的常数:
$$ \begin{align} \min_\phi \text{Reconstruct Loss} &= \max_\phi \mathbb{E}_{z \sim q(z|x)}[\ln p_\phi(x|z)] \\ &= \max_\phi \mathbb{E}_{z \sim q(z|x)}[\ln \mathcal{N}(\mu_\phi(z), \sigma_\phi(z)^2)] \\ &= \max_\phi \mathbb{E}_{z \sim q(z|x)}[\ln \frac{1}{\sqrt{2\pi} \sigma_\phi(z)} \exp(-\frac{(x - \mu_\phi(z))^2}{2\sigma_\phi(z)^2})] \\ &= \max_\phi \mathbb{E}_{z \sim q(z|x)}[-\ln \sqrt{2\pi} - \ln \sigma_\phi(z) - \frac{(x - \mu_\phi(z))^2}{2\sigma_\phi(z)^2}] \\ &\cong \max_\phi \sum_i^N [-\ln \sqrt{2\pi} - \ln \sigma_\phi(z_i) - \frac{(x_i - \mu_\phi(z_i))^2}{2\sigma_\phi(z_i)^2}] \\ &= \min_\phi \sum_i^N [\ln \sqrt{2\pi} + \ln \sigma_\phi(z_i) + \frac{(x_i - \mu_\phi(z_i))^2}{2\sigma_\phi(z_i)^2}] \\ &= \min_\phi \sum_i^N [\ln \sigma_\phi(z_i) + \frac{(x_i - \mu_\phi(z_i))^2}{2\sigma_\phi(z_i)^2}] \\ &= \min_\phi \sum_i^N {(x_i - \mu_\phi(z_i))^2} \end{align} $$在 $(17)$ 中,我们将期望的计算替换为采样的估算,从而允许训练集加入计算。每次训练中 $z$ 的样本都来自 $q(z|x)$ 的分布,在训练中是可以离散地枚举到的。
在 $(19)$ 中,将 $\sigma_\phi(z)$ 代入作为常数,最后的式子就等于最小二乘了,使生成的图片的每个像素点与原始图片的像素点做比较。
Final Thought
到这里我们推的公式已经和上篇文章的损失函数完全一致了,优化 ELBO 一举两得,既让编码器的输出更接近正态分布,也能让解码器生成的图片更接近原始图片。
(不过我还是不大明白这个推导过程是先有变分推理后有损失函数式子,还是先有损失函数式子这个射中的箭再往回画的推导过程的靶子)。