Flaneur2020

/home

/中文

/links

Notes on Variational Autoencoder

前段时间想学习一下 Stable Diffusion，不过发现好像需要先弄懂 VAE （Variational Autoencoder）是咋回事。这里先记一下对 VAE 的朴素理解，ELBO 数学还大看明白，后面单独记一下。

《Intuitively Understanding Variational Autoencoders》这篇文章讲 VAE 背后的 intuition 讲的很不错，这里就相当于人肉总结的性质。

Autoencoder

在看 VAE 之前，先回顾下更古早的 Autoencoder 这个模型：

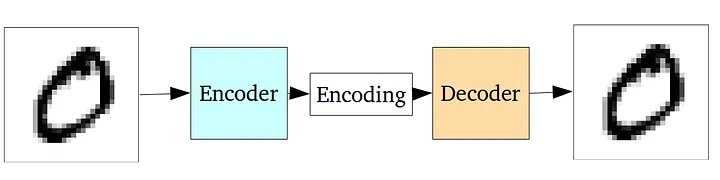
Autoencoder 由两个神经网络组成，左侧的神经网络叫做 Encoder，它能够将输入的图片转成一个低维度的 Encoding 向量（也称作 Latent 向量），右侧的神经网络叫做 Decoder，它负责拿 Encoding 作为输入，还原回来原始的图像。

相当于一个压缩与解压缩的过程。

Encoding 相比原始图片要小的多，通过这个小小的 Encoding 向量，又怎能还原回复杂的原始图像呢？

我们在学习使用神经网络做数字识别时，有一个 intuition 是，面对一个手写输入的 64 x 64 像素的图片，一部分浅层神经元擅长识别「撇」，一部分浅层神经元擅长识别「捺」，每经过神经网络的一层，特征提取的越高级，最终对应一个 10 维的输出。

这个 intuition 也可以拿来理解 Autoencoder 是怎样工作的：Encoder 的神经元识别「撇」「捺」「横」「竖」等画图的构造乃至更为高层、内在的特征，把这部分信息放在 Encoding 里，Encoder 的神经元则学习怎样用这些「撇」「捺」「横」「竖」参考着更高级的特征来画成图。

由于 Encoding 向量的维度受限，整个 Autoencoder 必须学会提取输入图片中最主要的特征，势必对输入的原始信息有一定取舍。这样一来，Encoder 在压缩输入数据时，实际上是在学习数据的内在结构和最重要的特征，有了这些特征，加上 Decoder 神经元掌握的「画法」，就能够尽可能地还原出原始的图像。

Autoencoder 的训练是无监督的，不需要做数据标注，直接将原始的输入与 Decoder 的最终输出做比较即可进行训练。它在训练中使用的损失函数称作 “Reconstruction Loss”，很简单计算下 MSE 即可：

def ae_loss(input, output):
	# compute the average MSE error, then scale it up i.e. simply sum on all axes
	reconstruction_loss = sum(square(output-input))
	return reconstruction_loss

Autoencoder 的局限

训练的好的 Autoencoder 的还原能力是很强的，可见它有很强的绘画能力。但是 Autoencoder 应用场景有限，只有少数图片降噪这种地方有用。

是什么限制了它的发挥？问题就出在 Encoding 向量对我们来讲是一个黑盒：Encoding 向量所在的 Latent space 很可能是离散的，不连续。

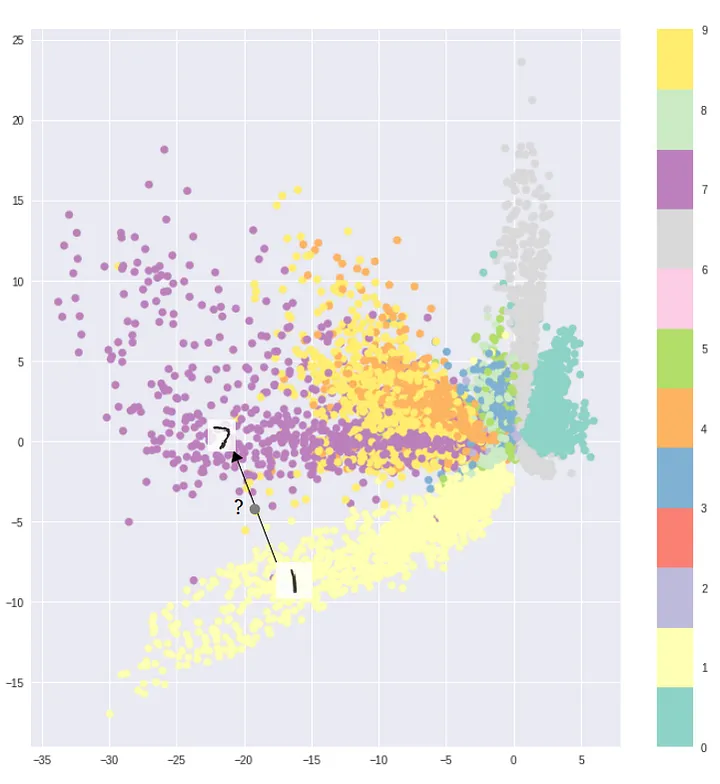
可见典型的 Encoding 之间是有一定聚类的。但是它们并不连续，导致我们不能编排一些我们的需求到 Encoding 向量中来指导 Autoencoder 的生成，也就无法将它作为生成模型来用。如果从 latent space 中随机采样一个向量，跑出来的大概率是噪音。

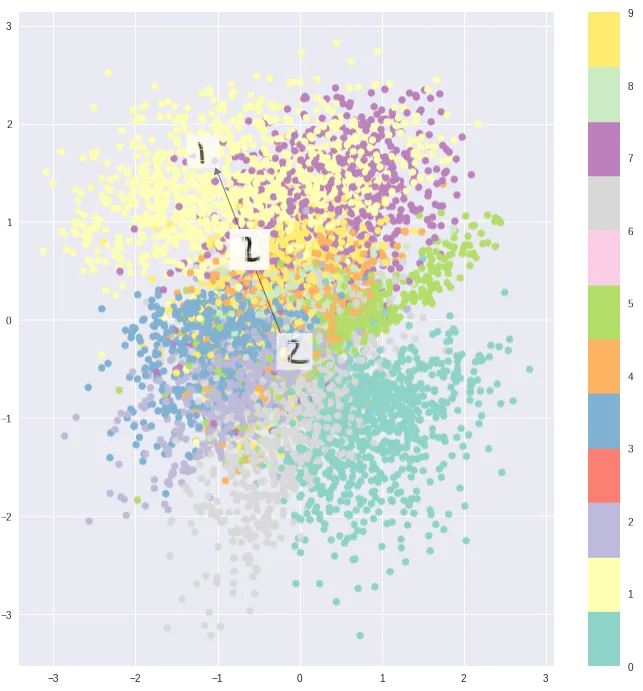
比较理想的状态是，整个 Latent space 能够连续，典型的 Encoding（比如数字 7 和 1 对应的 Encoding）有聚类，在聚类与聚类的边缘采样，能够生成出来含糊的「渐变」流形而不是噪音乱码：

引入 Sampling

VAE 就是解决了这个问题的 Autoencoder。它的 Latent space 是完全连续的，允许随机抽样生成，也可以与文本 Embedding 做对接，就可以做些有用的生成了。

怎样让 Latent space 做到连续？

首先要解决的问题是，在 Autoencoder 中每个特征都是呈点状的，搞不好稍微差一点点位置，Decoder 画出来的图就南辕北辙。

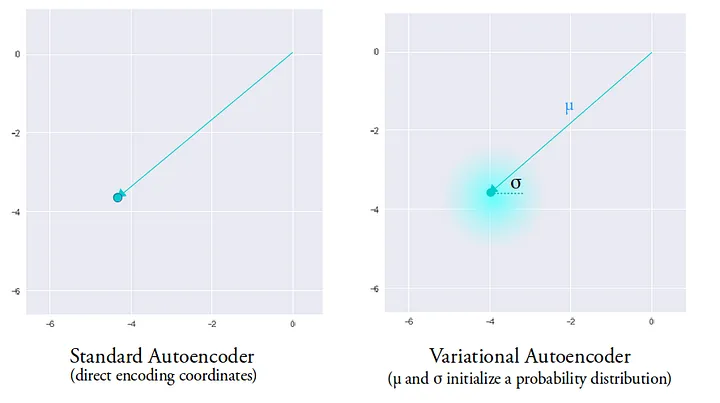
VAE 使用两个向量 $\mu$ 和 $\sigma$ 来替代呈点状的 Encoding 向量，并增加了一个 Sample 阶段。$\mu$ 和 $\sigma$ 对应一个正态分布中的平均值和标准差，Sample 就是在这个正态分布中进行采样。

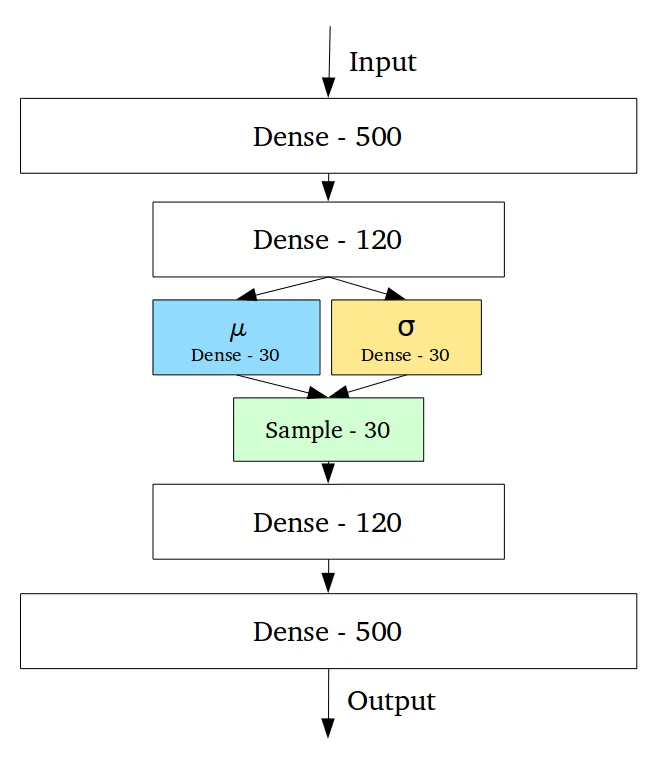
这一来，在训练中 Decoder 能够不那么对点状的 Encoding 向量非此莫属、太过敏感，而是在一个球心是 $\mu$ 半径是 $\sigma$ 的椭圆球空间范围内，都可以还原出图。

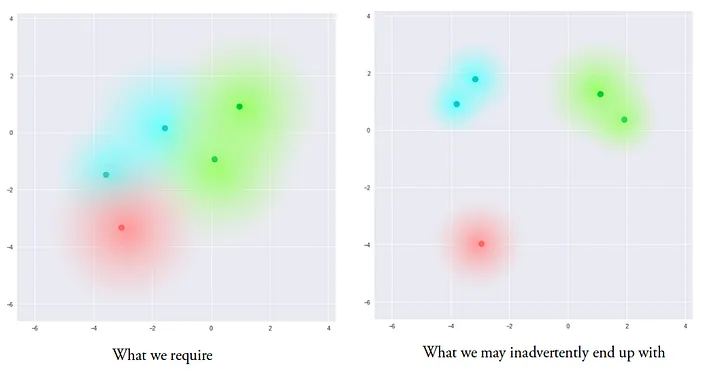
但是神经网络在训练时候仍有可能找到奇怪的偷懒路径，在广大的 Latent space 中，不同的分布之间仍可能距离非常遥远：

KL 散度

VAE 让 Latent space 整体变得连续的思路是，让整个 Latent space 尽量接近一个均值为 0、标准差为 1 的正态分布 $Normal(0, 1)$。

KL 散度（Kullback–Leibler divergence）可以用于衡量两个概率分布之间的差异。比较两个正态分布的 KL 散度的公式是：

$$ D_{KL}(P \parallel Q) = \log \frac{\sigma_Q}{\sigma_P} + \frac{\sigma_P^2 + (\mu_P - \mu_Q)^2}{2\sigma_Q^2} - \frac{1}{2} $$

代入均值为 0、标准差为 1 作为要比较的另一个概率分布，针对 $\mu$ 和 $\sigma$ 两个向量来计算 KL 散度的公式是：

$$ \sum_{i=1}^{n} \sigma_{i}^{2} + \mu_{i}^{2} - \log(\sigma_{i}) - 1 $$

不过我们在训练中吗需要比较的不是一个正态分布到 $Normal(0, 1)$，而是 N 个正态分布到 $Normal(0,1)$ 的总的差异。这里好像相当于将所有的 KL 散度对比加在一起，仍能反映总的分布和 $Normal(0, 1)$ 的差异，这里可能会有些数学推导还没有看懂，到后面再看好了。

通过把 KL 散度放到损失函数中，也就相当于起到正则化的作用，最终得到这个完整的损失函数：

def vae_loss(input_img, output, log_stddev, mean):
	# compute the average MSE error, then scale it up i.e. simply sum on all axes
	reconstruction_loss = sum(square(output-input_img))
	# compute the KL loss
	kl_loss = -0.5 * sum(1 + log_stddev - square(mean) - square(exp(log_stddev)), axis=-1)
	# return the average loss over all images in batch
	total_loss = mean(reconstruction_loss + kl_loss)
	return total_loss

套上 KL 散度之后，训练出来的 Latent space 按说就是比较接近我们想要的分布形状了：

back to top