与 RNN 自带顺序不同,Transformer 需要为序列额外引入一个顺序编码(Positional Encoding),它的维度和 embedding 向量的维度相同,与 embedding 向量加在一起来引进顺序信息。
不过 Transformer 原始论文中的 Positional Encoding 看起来像是魔法:
$$ \begin{equation} PE(k) = \begin{bmatrix} sin(k) \\ cos(k) \\ sin(\frac{k}{10000^{2/d}}) \\ cos(\frac{k}{10000^{2/d}}) \\ sin(\frac{k}{10000^{4/d}}) \\ cos(\frac{k}{10000^{4/d}}) \\ \vdots \\ sin(\frac{k}{10000^{ (d - 2) / d}}) \\ cos(\frac{k}{10000^{ (d - 2) / d}}) \end{bmatrix} _{d \times 1} \end{equation} $$代入到公式是这样写:
$$ \begin{align} PE(k,2j) &= sin(\frac{k}{10000^{2j/d}}),\\ PE(k,2j+1) &= cos(\frac{k}{10000^{2j/d}}). \end{align} $$为什么 sin 和 cos 函数能够表示顺序?
时钟
能代入的一个 Intuition 是,我们看时间用的时钟就是 sin、cos 函数表示位置的一个实例。
在时钟里,秒针、分针、时针就代表了一个位置向量,03:01:00 作为一个位置显然是大于 02:44:30 的。
如果用时钟作为位置编码的话,就对应到一个 6 维的向量,因为使用三角函数表示角度的话,需要一个二维向量 $[sin(x) \space cos(x)]$,三个角度就得用一个 6 维向量来表示:
$$ \begin{equation} PE_{clock}(k) = \begin{bmatrix} sin(2 \pi k) \\ cos(2 \pi k) \\ sin(\frac{2 \pi k}{3600}) \\ cos(\frac{2 \pi k}{3600}) \\ sin(\frac{2 \pi k}{3600 * 12}) \\ cos(\frac{2 \pi k}{3600 * 12}) \\ \end{bmatrix} _{6 \times 1} \end{equation} $$在秒针转动时,分针与时针也会轻微转动,不过秒针、分针、时针的频率会按依次递减。比如秒针每转动 3600 圈,分针才会转完一圈,分针转完 12 圈,时针转完一圈。
如果要增加维度,就加入天、星期、月、年等更高的单位就可以了。
不过时钟这个例子有点不完美的地方是时钟每维的增长幅度不大规律。假设有一个外星时钟是不同维度皆为固定的 3600 倍数周期:
$$ \begin{align} PE(k,2j) &= sin(\frac{k}{3600^{2j}}),\\ PE(k,2j+1) &= cos(\frac{k}{3600^{2j}}). \end{align} $$到这里和 Transformer 的公式已经很接近了,不同在于这里的频率是指数递减,而 Transformer 的公式在指数项中除以了一个 $d$:$sin(\frac{k}{3600^{2j/d}})$。如果不除 $d$ 的话,位置向量维度间频率的衰减太快,容易使得位置向量中除了前两个位置有数以外,其他维度都是接近于零,真正参与位置编码的维度就太少了。除以 $d$ 之后,每下一个维度比前一个维度的频率低个 1.2 倍这种,信息的冗余度也更高?
到这里还有一个问题,为什么 Transformer 设置的常量是 10000?
使用类似时钟表示位置有一个问题是时钟是循环的,00:00:00 和 12:59:59 孰大孰小?而且会导致判断距离时候出问题,12:59:59 和 00:00:01 的距离比 00:00:01 到 00:05:01 的距离更近。所以会希望尽量不要走完这个圆圈,只用半个圆圈来计算距离就相对不容易出事。至于为什么选择 10000,猜应该就是试出来的了,按说上下文长度更长的话,会把这个数字再调大?
二进制位置编码
关于位置编码的另一个 Intuition 是二进制,比如:
| num | binary (big endian) |
|---|---|
| 1 | 1000 |
| 2 | 0100 |
| 3 | 1100 |
| 4 | 0010 |
| 5 | 1010 |
| 6 | 0110 |
按大端排列的话,可以发现 bit 位置越低,0 与 1 轮换的频率越低。
为什么 Transformer 没有使用 0 和 1 组成的向量来表示位置呢?文章 [2] 说因为要跟 Embedding 向量相加,希望位置向量中的数值尽量是 -1.0 ~ 1.0 之间的数值。这个问题不算大,稍微做下变换 $f(x)=2x-1$ 就到 -1.0~1.0 之间了。
更大的问题是 0 和 1 的编码是一个离散值,好像说不利于学习,这块就不大懂了。不过直观上,使用二进制编码也有类似前面说的 $3600^{2j}$ 这样指数衰减的问题。再一个就是信息的冗余度不如三角函数曲线高,理论上你只看时针也能得出来秒针在什么位置的信息,反观二进制编码丢了一个 bit 距离就差远了。
Positional Encoding Matrix
在讲 Positional Encoding 的文章中经常见到这样的图:
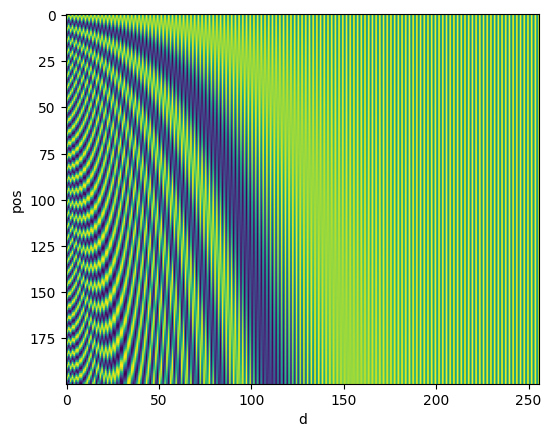
但是第一次看这个图也是很懵的,该怎样理解这张图?
横轴是维度数,纵轴是位置编号。正确的阅读方法不是关注里面这个蓝波和绿波,而是关注每个维度中蓝绿切换的频率。维度越高,对应的蓝绿切换的频率越低。这点也是二进制位置中可以观察到的性质。
此外常见的一张图是看距离向量之间的距离 Matrix:
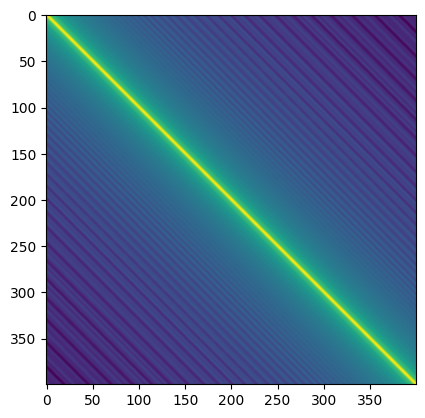
从这张图里可以看出大致上两个距离向量之间的距离越近,颜色越浅,反之颜色越深。这里体现的是相对距离的性质:两个相等的位置偏移量之间的距离总是相等的。这个性质好像有一个关于线性变换的证明,在这里就不记了。
Transformer 在计算 Attention 时做的是矩阵相乘,而矩阵相乘能体现出两边的距离。按说 Transformer 会更关注两个 Embedding 向量之间的相对距离,而未必那么关心绝对的位置。
这两张图可以通过下面的代码在 notebook 中复现:
from matplotlib import pyplot as plt
import numpy as np
def sinPosition(pos, d=256, n=10000):
p = np.zeros(d)
for i in np.arange(int(d/2)):
denominator = np.power(n, 2*i/d)
p[2*i] = np.sin(pos/denominator)
p[2*i+1] = np.cos(pos/denominator)
return p
pe = np.array([sinPosition(i) for i in range(200)])
distances = pe.dot(pe.T)
plt.imshow(pe)
plt.xlabel('d')
plt.ylabel('pos')
plt.show()
plt.imshow(distances)
plt.show()
总结
- 可以将时钟和二进制作为理解三角函数位置编码的 Intuition,这两个 Intuition 中都能显示“位置向量中越高维度的值,其频率越低”的性质;
- 三角函数位置编码可以适应特定长度的维度数,相比于二进制编码,它的取值范围比较好地分布在 -1.0 ~ 1.0 中,是连续的值,而且信息冗余度高;
- 三角函数位置编码可以体现出相对距离的性质,对于固定的位置偏移数总是有同样的距离;