高阶函数
haskell中的函数可以作为参数和返回值传来传去，这样的函数就被称作高阶函数。高阶函数可不只是某简单特性而已，它贯穿于haskell的方方面面。要拒绝循环与状态的改变而通过定义问题"是什么"来解决问题，高阶函数必不可少。它们是编码的得力工具。
柯里函数
本质上，haskell的所有函数都只有一个参数，那么我们先前编那么多含有多个参数的函数又是怎么回事? 呵，小伎俩! 所有多个参数的函数都是柯里函数。 什么意思呢? 取一个例子最好理解，就拿我们的好朋友max函数说事吧。它看起来像是取两个参数，返回较大的那个数。 实际上，执行max 4 5时，它会首先返回一个取一个参数的函数，其返回值不是4就是该参数，取决于谁大。 然后，以5为参数调用它，并取得最终结果。 这听着挺绕口的，不过这一概念十分的酷! 如下的两个调用是等价的：
ghci> max 4 5 5 ghci> (max 4) 5 5
把空格放到两个东西之间，称作函数调用。它有点像个运算符，并拥有最高的优先级。 看看max函数的类型:max :: (Ord a) => a -> a -> a。 也可以写作:max :: (Ord a) => a -> (a -> a)。 可以读作max取一个参数a，并返回一个函数(就是那个->)，这个函数取一个a类型的参数，返回一个a。 这便是为何只用箭头来分隔参数和返回值类型。
这样的好处又是如何? 简言之，我们若以不全的参数来调用某函数，就可以得到一个不全调用的函数。 如果你高兴，构造新函数就可以如此便捷，将其传给另一个函数也是同样方便。
看下这个函数，简单至极:
multThree :: (Num a) => a -> a -> a -> a multThree x y z = x * y * z
我们若执行mulThree 3 5 9或((mulThree 3) 5) 9，它背后是如何运作呢？ 首先，按照空格分隔，把3交给mulThree。 这返回一个返回函数的函数。 然后把5交给它，返回一个取一个参数并使之乘以15的函数。 最后把9交给这一函数，返回135。 想想，这个函数的类型也可以写作multThree :: (Num a) => a -> (a -> (a -> a))，->前面的东西就是函数取的参数，后面的东西就是其返回值。 所以说，我们的函数取一个a，并返回一个类型为(Num a) => a -> (a -> a)的函数，类似，这一函数返回一个取一个a，返回一个类型为(Num a) => a -> a的函数。 而最后的这个函数就只取一个a并返回一个a，如下:
ghci> let multTwoWithNine = multThree 9 ghci> multTwoWithNine 2 3 54 ghci> let multWithEighteen = multTwoWithNine 2 ghci> multWithEighteen 10 180
前面提到，以不全的参数调用函数可以方便地创造新的函数。例如，搞个取一数与100比较大小的函数该如何? 大可这样:
compareWithHundred :: (Num a，Ord a) => a -> Ordering compareWithHundred x = compare 100 x
用99调用它，就可以得到一个GT。 简单。 注意下在等号两边都有x。 想想compare 100会返回什么？一个取一数与100比较的函数。 Wow，这不正是我们想要的? 这样重写:
compareWithHundred :: (Num a，Ord a) => a -> Ordering compareWithHundred = compare 100
类型声明依然相同，因为compare 100返回函数。 compare的类型为(Ord a) => a -> (a -> Ordering)，用100调用它后返回的函数类型为(Num a，Ord a) => a -> Ordering，同时由于100还是Num类型类的实例，所以还得另留一个类约束。
Yo! 你得保证已经弄明白了柯里函数与不全调用的原理，它们很重要！
中缀函数也可以不全调用，用括号把它和一边的参数括在一起就行了。 这返回一个取一参数并将其补到缺少的那一端的函数。 一个简单函数如下:
divideByTen :: (Floating a) => a -> a divideByTen = (/10)
调用divideByTen 200就是(/10) 200，和200 / 10等价。
一个检查字符是否为大写的函数:
isUpperAlphanum :: Char -> Bool isUpperAlphanum = (`elem` ['A'..'Z'])
唯一的例外就是-运算符，按照前面提到的定义，(-4)理应返回一个并将参数减4的函数，而实际上，处于计算上的方便，(-4)表示负4。 若你一定要弄个将参数减4的函数，就用subtract好了，像这样(subtract 4).
若不用let给它命名或传到另一函数中，在ghci中直接执行multThree 3 4会怎样?
ghci> multThree 3 4 :1:0: No instance for (Show (t -> t)) arising from a use of `print' at :1:0-12 Possible fix: add an instance declaration for (Show (t -> t)) In the expression: print it In a 'do' expression: print it
ghci说，这一表达式返回了一个a -> a类型的函数，但它不知道该如何显示它。 函数不是Show类型类的实例，所以我们不能得到表示一函数内容的字符串。 若在ghci中计算1+1，它会首先计算得2，然后调用show 2得到该数值的字符串表示，即"2"，再输出到屏幕.
是时候了，来点高阶函数！
haskell中的函数可以取另一个函数做参数，也可以返回函数。 举个例子，我们弄个取一个函数并调用它两次的函数.
applyTwice :: (a -> a) -> a -> a applyTwice f x = f (f x)
首先注意这类型声明。 在此之前我们很少用到括号，因为(->)是自然的右结合，不过在这里括号是必须的。 它标明了首个参数是个参数与返回值类型都是a的函数，第二个参数与返回值的类型也都是a。 我们可以用柯里函数的思路来理解这一函数，不过免得自寻烦恼，我们姑且直接把它看作是取两个参数返回一个值，其首个参数是个类型为(a->a)的函数,第二个参数是个a。 该函数的类型可以是(Int->Int)，也可以是(String->String)，但第二个参数必须与之一致。
Note: 现在开始我们会直说某函数含有多个参数(除非它真的只有一个参数)。 以简洁之名，我们会说(a->a->a)取两个参数，尽管我们知道它在背后做的手脚.
这个函数是相当的简单，就拿参数f当函数，用x调用它得到的结果再去调用它。 也就可以这样玩:
ghci> applyTwice (+3) 10
16
ghci> applyTwice (++ " HAHA") "HEY"
"HEY HAHA HAHA"
ghci> applyTwice ("HAHA " ++) "HEY"
"HAHA HAHA HEY"
ghci> applyTwice (multThree 2 2) 9
144
ghci> applyTwice (3:) [1]
[3,3,1]看，不全调用多神奇! 如果有个函数要我们给它传个一元函数，大可以不全调用一个函数让它剩一个参数，再把它交出去。
接下来我们用高阶函数的编程思想来实现个标准库中的函数，它就是zipWith。 它取一个函数和两个List做参数，并把两个List交到一起(使相应的元素去调用该函数)。 如下就是我们的实现:
zipWith' :: (a -> b -> c) -> [a] -> [b] -> [c] zipWith' _ [] _ = [] zipWith' _ _ [] = [] zipWith' f (x:xs) (y:ys) = f x y : zipWith' f xs ys
看下这个类型声明，它的首个参数是个函数，取两个参数处理交叉，其类型不必相同，不过相同也没关系。 第二三个参数都是List，返回值也是个List。 第一个List中元素的类型必须是a，因为这个处理交叉的函数的第一个参数是a。 第二个List中元素的类型必为b，因为这个处理交叉的函数第二个参数的类型是b。 返回的List中元素类型为c。 如果一个函数说取一个类型为a->b->c的函数做参数，传给它个a->a->c类型的也是可以的，但反过来就不行了。 可以记下，若在使用高阶函数的时候不清楚其类型为何，就先忽略掉它的类型声明，再到ghci下用:t命令来看下haskell的类型推导.
这函数的行为与普通的zip很相似，边界条件也是相同，只不过多了个参数，即处理元素交叉的函数。它关不着边界条件什么事儿，所以我们就只留一个_ 。后一个模式的函数体与zip也很像，只不过这里是f x y而非(x,y)。 只要足够通用，一个简单的高阶函数可以在不同的场合反复使用。 如下便是我们zipWith'函数本领的冰山一角:
ghci> zipWith' (+) [4,2,5,6] [2,6,2,3] [6,8,7,9] ghci> zipWith' max [6,3,2,1] [7,3,1,5] [7,3,2,5] ghci> zipWith' (++) ["foo "，"bar "，"baz "] ["fighters"，"hoppers"，"aldrin"] ["foo fighters","bar hoppers","baz aldrin"] ghci> zipWith' (*) (replicate 5 2) [1..] [2,4,6,8,10] ghci> zipWith' (zipWith' (*)) [[1,2,3],[3,5,6],[2,3,4]] [[3,2,2],[3,4,5],[5,4,3]] [[3,4,6],[9,20,30],[10,12,12]]
如你所见，一个简单的高阶函数就可以玩出很多花样。 命令式语言使用for、while、赋值、状态检测来实现功能，再包起来留个接口，使之像个函数一样调用。而函数式语言使用高阶函数来抽象出常见的模式，像成对遍历并处理两个List或从中筛掉自己不需要的结果。
接下来实现标准库中的另一个函数flip，flip简单地取一个函数作参数并返回一个相似的函数，只是它们的两个参数倒了个。
flip' :: (a -> b -> c) -> (b -> a -> c)
flip' f = g
where g x y = f y x从这类型声明中可以看出，它取一个函数，其参数类型分别为a和b，而它返回的函数的参数类型为b和a。 由于函数默认都是柯里化的，->为右结合，这里的第二对括号其实并无必要，(a -> b -> c) -> (b -> a -> c)与(a -> b -> c) -> (b -> (a -> c))等价,也与(a -> b -> c) -> b -> a -> c等价。 前面我们写了g x y = f y x，既然这样可行，那么f y x = g x y不也一样? 这一来我们可以改成更简单的写法:
flip' :: (a -> b -> c) -> b -> a -> c flip' f y x = f x y
在这里我们就利用了柯里函数的优势，只要调用flip' f而不带y和x，它就会返回一个俩参数倒个的函数。flip处理的函数往往都是用来传给其他函数调用，于是我们可以发挥柯里函数的优势，预先想好发生完全调用的情景并处理好返回值.
ghci> flip' zip [1,2,3,4,5] "hello"
[('h',1),('e',2),('l',3),('l',4),('o',5)]
ghci> zipWith (flip' div) [2,2..] [10,8,6,4,2]
[5,4,3,2,1]map 与 filter
map取一个函数和List做参数，遍历该List的每个元素来调用该函数产生一个新的List。 看下它的类型声明和实现:
map :: (a -> b) -> [a] -> [b] map _ [] = [] map f (x:xs) = f x : map f xs
从这类型声明中可以看出，它取一个取a返回b的函数和一组a的List，并返回一组b。 这就是haskell的有趣之处：有时只看类型声明就能对函数的行为猜个大致。map函数多才多艺，有一百万种用法。 如下是其中一小部分:
ghci> map (+3) [1,5,3,1,6] [4,8,6,4,9] ghci> map (++ "!") ["BIFF"，"BANG"，"POW"] ["BIFF!","BANG!","POW!"] ghci> map (replicate 3) [3..6] [[3,3,3],[4,4,4],[5,5,5],[6,6,6]] ghci> map (map (^2)) [[1,2],[3,4,5,6],[7,8]] [[1,4],[9,16,25,36],[49,64]] ghci> map fst [(1,2),(3,5),(6,3),(2,6),(2,5)] [1,3,6,2,2]
你可能会发现，以上的所有代码都可以用List Comprehension来替代。map (+3) [1,5,3,1,6]与[x+3 | x <- [1,5,3,1,6]完全等价。
filter函数取一个限制条件和一个List，返回该List中所有符合该条件的元素。 它的类型声明及实现大致如下:
filter :: (a -> Bool) -> [a] -> [a]
filter _ [] = []
filter p (x:xs)
| p x = x : filter p xs
| otherwise = filter p xs很简单。 只要p x所得的结果为真，就将这一元素加入新List，否则就无视之。几个使用范例:
ghci> filter (>3) [1,5,3,2,1,6,4,3,2,1] [5,6,4] ghci> filter (==3) [1,2,3,4,5] [3] ghci> filter even [1..10] [2,4,6,8,10] ghci> let notNull x = not (null x) in filter notNull [[1,2,3],[],[3,4,5],[2,2],[],[],[]] [[1,2,3],[3,4,5],[2,2]] ghci> filter (`elem` ['a'..'z']) "u LaUgH aT mE BeCaUsE I aM diFfeRent" "uagameasadifeent" ghci> filter (`elem` ['A'..'Z']) "i lauGh At You BecAuse u r aLL the Same" "GAYBALLS"
同样，以上都可以用List Comprehension的限制条件来实现。 并没有教条规定你必须在什么情况下用map和filter还是List Comprehension，选择权归你，看谁舒服用谁就是。 如果有多个限制条件，只能连着套好几个filter或用&&等逻辑函数的组合之，这时就不如list comprehension来得爽了。
还记得上一章的那个quicksort函数么? 我们用到了List Comprehension来过滤大于或小于锚的元素。 换做filter也可以实现，而且更加易读：
quicksort :: (Ord a) => [a] -> [a]
quicksort [] = []
quicksort (x:xs) =
let smallerSorted = quicksort (filter (<x) xs)
biggerSorted = quicksort (filter (>x) xs)
in smallerSorted ++ [x] ++ biggerSorted
map和filter是每个函数式程序员的面包黄油（呃，map和filter还是List Comprehension并不重要）。 想想前面我们如何解决给定周长寻找合适直角三角形的问题的? 在命令式编程中，我们可以套上三个循环逐个测试当前的组合是否满足条件，若满足，就打印到屏幕或其他类似的输出。 而在函数式编程中，这行就都交给map和filter。 你弄个取一参数的函数，把它交给map过一遍List，再filter之找到合适的结果。 感谢haskell的惰性，即便是你多次map一个list也只会遍历一遍该list，要找出小于100000的数中最大的3829的倍数，只需过滤结果所在的list就行了.
要找出小于100000的3829的所有倍数，我们应当过滤一个已知结果所在的list.
largestDivisible :: (Integral a) => a
largestDivisible = head (filter p [100000,99999..])
where p x = x `mod` 3829 == 0首先， 取一个降序的小于100000所有数的List，然后按照限制条件过滤它。 由于这个List是降序的，所以结果List中的首个元素就是最大的那个数。 惰性再次行动! 由于我们只取这结果List的首个元素，所以它并不关心这List是有限还是无限的，在找到首个合适的结果处运算就停止了。
接下来，我们就要找出所有小于10000的奇数的平方和，得先提下takeWhile函数，它取一个限制条件和List作参数，然后从头开始遍历这一List，并返回符合限制条件的元素。 而一旦遇到不符合条件的元素，它就停止了。 如果我们要取出字符串"elephants know how to party"中的首个单词，可以takeWhile (/=' ') "elephants know how to party"，返回"elephants"。 okay，要求所有小于10000的奇数的平方的和，首先就用(^2)函数map掉这个无限的List[1..]。然后过滤之，只取奇数就是了。 在大于10000处将它断开，最后前面的所有元素加到一起。 这一切连写函数都不用，在ghci下直接搞定.
ghci> sum (takeWhile (<10000) (filter odd (map (^2) [1..]))) 166650
不错! 先从几个初始数据(表示所有自然数的无限list)，再map它，filter它，切它，直到它符合我们的要求，再将其加起来。 这用list comprehension也是可以的，而哪种方式就全看你的个人口味.
ghci> sum (takeWhile (<10000) [m | m <- [n^2 | n <- [1..]], odd m]) 166650
感谢haskell的惰性特质，这一切才得以实现。 我们之所以可以map或filter一个无限list，是因为它的操作不会被立即执行，而是拖延一下。 只有我们要求haskell交给我们sum的结果的时候，sum函数才会跟takeWhile说，它要这些数。takeWhile就再去要求filter和map行动起来，并在遇到大于等于10000时候停止.
下个问题与Collatz序列有关，取一个自然数，若为偶数就除以2。 若为奇数就乘以3再加1。 再用相同的方式处理所得的结果，得到一组数字构成的的链。 它有个性质，无论任何以任何数字开始，最终的结果都会归1。 所以若拿13当作起始数，就可以得到这样一个序列13，40，20，10，5，16，8，4，2，1。13*3+1得40，40除2得20，如是继续，得到一个10个元素的链。
好的，我们想知道的是: 以1到100之间的所有数作为起始数，会有多少个链的长度大于15?
chain :: (Integral a) => a -> [a]
chain 1 = [1]
chain n
| even n = n:chain (n `div` 2)
| odd n = n:chain (n*3 + 1)该链止于1，这便是边界条件。 标准的递归函数:
ghci> chain 10 [10,5,16,8,4,2,1] ghci> chain 1 [1] ghci> chain 30 [30,15,46,23,70,35,106,53,160,80,40,20,10,5,16,8,4,2,1]
yay! 貌似工作良好。 现在由这个函数来告诉我们结果:
numLongChains :: Int
numLongChains = length (filter isLong (map chain [1..100]))
where isLong xs = length xs > 15我们把chain函数map到[1..100]，得到一组链的list，然后用个限制条件过滤长度大于15的链。 过滤完毕后就可以得出结果list中的元素个数.
Note: 这函数的类型为
numLongChains :: Int。 这是由于历史原因，length返回一个Int而非Num的成员类型，若要得到一个更通用的Num a，我们可以使用fromInterval函数来处理所得结果.
用map，我们可以写出类似map (*) [0..]之类的代码。 如果只是为了例证柯里函数和不全调用的函数是真正的值及其原理，那就是你可以把函数传递或把函数装在list中(只是你还不能将它们转换为字符串)。 迄今为止，我们还只是map单参数的函数到list，如map (*2) [0..]可得一组类型为(Num a) => [a]的list，而map (*) [0..]也是完全没问题的。*的类型为(Num a) -> a -> a -> a，用单个参数调用二元函数会返回一个一元函数。 如果用*来map 一个[0..]的list，就会得到一组一元函数组成的list，即(Num a) => [a->a]。map (*) [0..]所得的结果写起来大约就是[(*0),(*1),(*2)..]
ghci> let listOfFuns = map (*) [0..] ghci> (listOfFuns !! 4) 5 20
取所得list的第四个元素可得一函数，与(*4)等价。 然后用5调用它，与(* 4) 5或4*5都是等价的.
lambda
lambda就是匿名函数。有些时候我们需要传给高阶函数一个函数，而这函数我们只会用这一次，这就弄个特定功能的lambda。编写lambda，就写个\（因为它看起来像是希腊字母的lambda--如果你斜视的厉害），后面是用空格分隔的参数，->后面就是函数体。通常我们都是用括号将其括起，要不然它就会占据整个右边部分。
向上5英寸左右，你会看到我们在numLongChain函数中用where语句声明了个isLong函数传递给了filter。好的，用lambda代替它。
numLongChains :: Int numLongChains = length (filter (\xs -> length xs > 15) (map chain [1..100]))
lambda是个表达式，因此我们可以任意传递。表达式(\xs -> length xs > 15)返回一个函数，它可以告诉我们一个list的长度是否大于15。
不熟悉柯里函数与不全调用的人们往往会写出很多lambda，而实际上大部分都是没必要的。例如，表达式map (+3) [1,6,3,2]与map (\x -> x+3) [1,6,3,2]等价，(+3)和(\x -> x+3)都是给一个数加上3。不用说，在这种情况下不用lambda要清爽的多。
和普通函数一样，lambda也可以取多个参数。
ghci> zipWith (\a b -> (a * 30 + 3) / b) [5,4,3,2,1] [1,2,3,4,5] [153.0,61.5,31.0,15.75,6.6]
同普通函数一样，你也可以在lambda中使用模式匹配，只是你无法为一个参数设置多个模式，如[]和(x:xs)。lambda的模式匹配若失败，就会引发一个运行时错误，所以慎用！
ghci> map (\(a,b) -> a + b) [(1,2),(3,5),(6,3),(2,6),(2,5)] [3,8,9,8,7]
一般情况下，lambda都是括在括号中，除非我们想要后面的整个语句都作为lambda的函数体。很有趣，由于有柯里化，如下的两段是等价的：
addThree :: (Num a) => a -> a -> a -> a addThree x y z = x + y + z
addThree :: (Num a) => a -> a -> a -> a addThree = \x -> \y -> \z -> x + y + z
这样的函数声明与函数体中都有->，这一来类型声明的写法就很明白了。当然第一段代码更易读，不过第二个函数使得柯里化更容易理解。
有些时候用这种语句写还是挺酷的，我觉得这应该是最易读的flip函数实现了：
flip' :: (a -> b -> c) -> b -> a -> c flip' f = \x y -> f y x
尽管这与flip' f x y = f y x等价，但它可以更明白地表示出它会产生一个新的函数。flip常用来处理一个函数，再将返回的新函数传递给map或filter。所以如此使用lambda可以更明确地表现出返回值是个函数，可以用来传递给其他函数作参数。
折叠纸鹤
回到当初我们学习递归的情景。我们会发现处理list的许多函数都有固定的模式，通常我们会将边界条件设置为空list，再引入(x:xs)模式，对单个元素和余下的list做些事情。这一模式是如此常见，因此haskell引入了一组函数来使之简化，也就是fold。它们与map有点像，只是它们返回的是单个值。
一个fold取一个二元函数，一个初始值（我喜欢管它叫累加值）和一个需要fold（折叠）的list。这个二元函数有两个参数，即累加值和list的首项（或尾项），返回值是新的累加值。然后，以新的累加值和新的list首项调用该函数，如是继续。到list遍历完毕时，只剩下一个累加值，也就是最终的结果。
首先看下foldl函数，也叫做左折叠。它从list的左端开始折叠，用初始值和list的头部调用这二元函数，得一新的累加值，并用新的累加值与list的下一个元素调用二元函数。如是继续。
我们再实现下sum，这次用fold替代那复杂的递归：
sum' :: (Num a) => [a] -> a sum' xs = foldl (\acc x -> acc + x) 0 xs
测试下，一二三～
ghci> sum' [3,5,2,1] 11
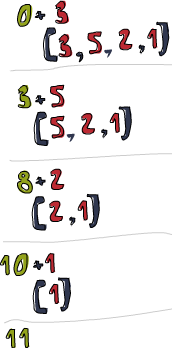
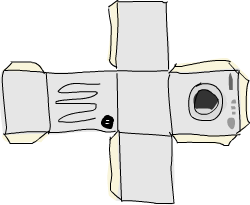
我们深入看下fold的执行过程：\acc x-> acc + x是个二元函数，0是初始值，xs是待折叠的list。一开始，累加值为0，当前项为3，调用二元函数0+3得3，作新的累加值。接着来，累加值为3，当前项为5，得新累加值8。再往后，累加值为8，当前项为2，得新累加值10。最后累加值为10，当前项为1，得11。恭喜，你完成了一次折叠(fold)！
左边的这个图表示了折叠的执行过程，一步又一步（一天又一天!）。浅棕色的数字都是累加值，你可以从中看出list是如何从左端一点点加到累加值上的。唔对对对！如果我们考虑到函数的柯里化，可以写出更简单的实现：
sum' :: (Num a) => [a] -> a sum' = foldl (+) 0
这个lambda函数(\acc x -> acc + x )与(+)等价。我们可以把xs等一应参数省略掉，反正调用foldl (+) 0会返回一个取list作参数的函数。通常，如果你的函数类似foo a = bar b a， 大可改为foo = bar b。有柯里化嘛。
呼呼，进入右折叠前我们再实现个用到左折叠的函数。大家肯定都知道elem是检查某元素是否属于某list的函数吧，我就不再提了（唔，刚提了）。用左折叠实现它:
elem' :: (Eq a) => a -> [a] -> Bool elem' y ys = foldl (\acc x -> if x == y then True else acc) False ys
好好好，这里我们有什么？起始值与累加值都是布尔值。在处理fold时，累加值与最终结果的类型总是相同的。如果你不知道怎样对待起始值，那我告诉你，我们先假设它不存在，以False开始。我们要是fold一个空list，结果就是False。然后我们检查当前元素是否为我们寻找的，如果是，就令累加值为True，如果否，就保留原值不变。若False，及表明当前元素不是。若True，就表明已经找到了。
右折叠foldr的行为与左折叠相似，只是累加值是从list的右边开始。同样，左折叠的二元函数取累加值作首个参数，当前值为第二个参数（即\acc x -> ...），而右折叠的二元函数参数的顺序正好相反（即\x acc -> ...）。这倒也正常，毕竟是从右端开始折叠。
累加值可以是任何类型，可以是数值，布尔值，甚至一个新的list。我们可以用右fold实现map函数，累加值就是个list。将map处理过的元素一个一个连到一起。很容易想到，起始值就是空list。
map' :: (a -> b) -> [a] -> [b] map' f xs = foldr (\x acc -> f x : acc) [] xs
如果我们用(+3)来映射[1,2,3]，它就会先到达list的右端，我们取最后那个元素，也就是3来调用(+3)，得6。追加(:)到累加值上，6:[]得[6]并成为新的累加值。用2调用(+3)，得5，追加到累加值，于是累加值成了[5,6]。再对1调用(+3)，并将结果4追加到累加值，最终得结果[4,5,6]。
当然，我们也完全可以用左折叠来实现它，map' f xs = foldl (\acc x -> acc ++ [f x]) [] xs就行了。不过问题是，使用(++)往list后面追加元素的效率要比使用(:)低得多。所以在生成新list的时候人们一般都是使用右折叠。
反转一个list，既也可以通过右折叠，也可以通过左折叠。有时甚至不需要管它们的分别，如sum函数的左右折叠实现都是十分相似。不过有个大的不同，那就是右折叠可以处理无限长度的数据结构，而左折叠不可以。将无限list从中断开执行左折叠是可以的，不过若是向右，就永远到不了头了。
所有遍历list中元素并据此返回一个值的操作都可以交给fold实现。无论何时需要遍历list并返回某值，都可以尝试下fold。因此，fold的地位可以说与map和filter并驾齐驱，同为函数式编程中最常用的函数之一。
foldl1与foldr1的行为与foldl和foldr相似，只是你无需明确提供初始值。他们假定list的首个（或末尾）元素作为起始值，并从旁边的元素开始折叠。这一来，sum函数大可这样实现：sum = foldl1 (+)。这里待折叠的list中至少要有一个元素，若使用空list就会产生一个运行时错误。不过foldl和foldr与空list相处的就很好。所以在使用fold前，应该先想下它会不会遇到空list，如果不会遇到，大可放心使用foldr1和foldl1。
为了体会fold的威力，我们就用它实现几个库函数：
maximum' :: (Ord a) => [a] -> a maximum' = foldr1 (\x acc -> if x > acc then x else acc) reverse' :: [a] -> [a] reverse' = foldl (\acc x -> x : acc) [] product' :: (Num a) => [a] -> a product' = foldr1 (*) filter' :: (a -> Bool) -> [a] -> [a] filter' p = foldr (\x acc -> if p x then x : acc else acc) [] head' :: [a] -> a head' = foldr1 (\x _ -> x) last' :: [a] -> a last' = foldl1 (\_ x -> x)
仅靠模式匹配就可以实现head函数和last函数，而且效率也很高。这里只是为了演示，用fold的实现方法。我觉得我们这个reverse'定义的相当聪明，用一个空list做初始值，并向左展开list，从左追加到累加值，最后得到一个反转的新list。\acc x -> x : acc有点像:函数，只是参数顺序相反。所以我们可以改成foldl (flip (:)) []。
有个理解折叠的思路：假设我们有个二元函数f，起始值z，如果从右折叠[3,4,5,6]，实际上执行的就是f 3 (f 4 (f 5 (f 6 z)))。f会被list的尾项和累加值调用，所得的结果会作为新的累加值传入下一个调用。假设f是(+)，起始值z是0，那么就是3 + (4 + (5 + (6 + 0)))，或等价的前缀形式：(+) 3 ((+) 4 ((+) 5 ((+) 6 0)))。相似，左折叠一个list，以g为二元函数，z为累加值，它就与g (g (g (g z 3) 4) 5) 6等价。如果用flip (:)作二元函数，[]为累加值（看得出，我们是要反转一个list），这就与flip (:) (flip (:) (flip (:) (flip (:) [] 3) 4) 5) 6等价。显而易见，执行该表达式的结果为[6,5,4,3]。
scanl和scanr与foldl和foldr相似，只是它们会记录下累加值的所有状态到一个list。也有scanl1和scanr1。
ghci> scanl (+) 0 [3,5,2,1] [0,3,8,10,11] ghci> scanr (+) 0 [3,5,2,1] [11,8,3,1,0] ghci> scanl1 (\acc x -> if x > acc then x else acc) [3,4,5,3,7,9,2,1] [3,4,5,5,7,9,9,9] ghci> scanl (flip (:)) [] [3,2,1] [[],[3],[2,3],[1,2,3]]
当使用scanl时，最终结果就是list的最后一个元素。而在scanr中则是第一个。
sqrtSums :: Int sqrtSums = length (takeWhile (<1000) (scanl1 (+) (map sqrt [1..]))) + 1
ghci> sqrtSums 131 ghci> sum (map sqrt [1..131]) 1005.0942035344083 ghci> sum (map sqrt [1..130]) 993.6486803921487
scan可以用来跟踪fold函数的执行过程。想想这个问题，取所有自然数的平方根的和，寻找在何处超过1000？先map sqrt [1..]，然后用个fold来求它们的和。但在这里我们想知道求和的过程，所以使用scan，scan完毕时就可以得到小于1000的所有和。所得结果list的第一个元素为1，第二个就是1+根2，第三个就是1+根2+根3。若有x个和小于1000，那结果就是x+1。
有$的函数调用
好的，接下来看看$函数。它也叫作函数调用符。先看下它的定义：
($) :: (a -> b) -> a -> b f $ x = f x
什么鬼东西？这没啥意义的操作符？它只是个函数调用符罢了？好吧，不全是，但差不多。普通的函数调用符有最高的优先级，而$的优先级则最低。用空格的函数调用符是左结合的，如f a b c与((f a) b) c等价，而$则是右结合的。
听着不错。但有什么用？它可以减少我们代码中括号的数目。试想有这个表达式：sum (map sqrt [1..130])。由于低优先级的$，我们可以将其改为sum $ map sqrt [1..130]，可以省敲不少键！sqrt 3 + 4 + 9会怎样？这会得到9，4和根3的和。若要取(3+4+9)的平方根，就得sqrt (3+4+9)或用$：sqrt $ 3+4+9。因为$有最低的优先级，所以你可以把$看作是在右面写一对括号的等价形式。
sum (filter (> 10) (map (*2) [2..10]))该如何？嗯，$是右结合，f (g (z x))与f $ g $ z x等价。所以我么可以将sum (filter (> 10) (map (*2) [2..10])重写为sum $ filter (> 10) $ map (*2) [2..10]。
除了减少括号外，$还可以将数据作为函数使用。例如映射一个函数调用符到一组函数组成的list：
ghci> map ($ 3) [(4+),(10*),(^2),sqrt] [7.0,30.0,9.0,1.7320508075688772]
函数组合
在数学中，函数组合是这样定义的：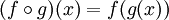
，表示组合两个函数成为一个函数。以x调用这一函数，就与用x调用g再用所得的结果调用f等价。
haskell中的函数组合与之很像，即.函数。其定义为：
(.) :: (b -> c) -> (a -> b) -> a -> c f . g = \x -> f (g x)
注意下这类型声明，f的参数类型必须与g的返回类型相同。所以得到的组合函数的参数类型与g相同，返回类型与f相同。表达式negate . (*3)返回一个求一数字乘以3后的负数的函数。
函数组合的用处之一就是生成新函数，并传递给其它函数。当然我们可以用lambda实现，但大多数情况下，使用函数组合无疑更直白。假设我们有一组由数字组成的list，要将其全部转为负数，很容易就想到应先取其绝对值，再取负数，像这样：
ghci> map (\x -> negate (abs x)) [5,-3,-6,7,-3,2,-19,24] [-5,-3,-6,-7,-3,-2,-19,-24]
注意下这个lambda与那函数组合是多么的相像。用函数组合，我们可以将代码改为：
ghci> map (negate . abs) [5,-3,-6,7,-3,2,-19,24] [-5,-3,-6,-7,-3,-2,-19,-24]
漂亮！函数组合是右结合的，我们同时组合多个函数。表达式f (g (z x))与(f . g . z) x等价。按照这个思路，我们可以将
ghci> map (\xs -> negate (sum (tail xs))) [[1..5],[3..6],[1..7]] [-14,-15,-27]
改为：
ghci> map (negate . sum . tail) [[1..5],[3..6],[1..7]] [-14,-15,-27]
不过含多个参数的函数该怎么办？好，我们可以使用不全调用使每个函数都只剩下一个参数。sum (replicate 5 (max 6.7 8.9))可以重写为(sum . replicate 5 . max 6.7) 8.9或sum . replicate 5 . max 6.7 $ 8.9。在这里会产生一个函数，它取与max 6.7同样的参数，并使用结果调用replicate 5再用sum求和。最后用8.9调用该函数。不过一般你可以这么读，用8.9调用max 6.7，然后使它replicate 5，再sum之。如果你打算用函数组合来替掉那堆括号，可以先在最靠近参数的函数后面加一个$，接着就用.组合其所有函数调用，而不用管最后那个参数。如果有这样一段代码：replicate 100 (product (map (*3) (zipWith max [1,2,3,4,5] [4,5,6,7,8])))，可以改为：replicate 100 . product . map (*3) . zipWith max [1,2,3,4,5] $ [4,5,6,7,8]。如果表达式以3个括号结尾，就表示你可以将其修改为函数组合的形式。
函数组合的另一用途就是定义point free style（也称作pointless style）的函数。就拿我们之前写的函数作例子：
sum' :: (Num a) => [a] -> a sum' xs = foldl (+) 0 xs
等号的两端都有个xs。由于有柯里化（Currying），我们可以省掉两端的xs。foldl (+) 0返回的就是一个取一list作参数的函数，我们把它修改为sum' = foldl (+) 0，这就是point free style。下面这个函数又该如何改成point free style呢？
fn x = ceiling (negate (tan (cos (max 50 x))))
像刚才那样简单去掉两端的x是不行的，函数体中x的右边还有括号。cos (max 50)是有错误的，你不能求一个函数的余弦。我们的解决方法就是，使用函数组合。
fn = ceiling . negate . tan . cos . max 50
漂亮！point free style会令你去思考函数的组合方式，而非数据的传递方式，更加简洁直白。你可以将一组简单的函数组合在一起，使之形成一个复杂的函数。不过函数若过于复杂，再使用point free style往往会适得其反，因此构造较长的函数组合链是不被鼓励的（虽然我本人热衷于函数组合）。更好的解决方法，就是使用let语句给中间的运算结果绑定一个名字，或者说把问题分解成几个小问题再组合到一起。这样一来我们代码的读者就可以轻松些，不必要纠结那巨长的函数组合链了。
在map和filter那节中，我们求了小于10000的所有奇数的平方的和。如下就是将其置于一个函数中的样子：
oddSquareSum :: Integer oddSquareSum = sum (takeWhile (<10000) (filter odd (map (^2) [1..])))
身为函数组合狂人，我可能会这么写：
oddSquareSum :: Integer oddSquareSum = sum . takeWhile (<10000) . filter odd . map (^2) $ [1..]
不过若是给别人看，我可能就这么写了：
oddSquareSum :: Integer
oddSquareSum =
let oddSquares = filter odd $ map (^2) [1..]
belowLimit = takeWhile (<10000) oddSquares
in sum belowLimit这段代码可赢不了代码花样大赛，不过我们的读者可能会觉得它比函数组合链更好看。